Introduction

I worked on “Port NMatrix to JRuby” in the context of the Google Summer of Code (GSoC) 2016 and I am pleased to announce that NMatrix can now be used in JRuby.

With JRuby NMatrix, a linear algebra library, wraps Apache Commons Math for its most basic functionalities. NMatrix supports dense matrices containing either doubles or Ruby objects as the data type. The performance of JRuby with Apache Commons Maths is quite satisfactory (see below for performance comparisons) even without making use of JRuby threading capabilities.

I have also ported the mixed_models gem, which uses NMatrix heavily at its core, to JRuby. This gem allowed us to test NMatrix-JRuby with real-life data.

This blog post summarizes my work on the project with SciRuby, and reports the final status of the project.

The original GSoC proposal, plan and application can be found here. Until merging is complete, commits are available here.

Performance

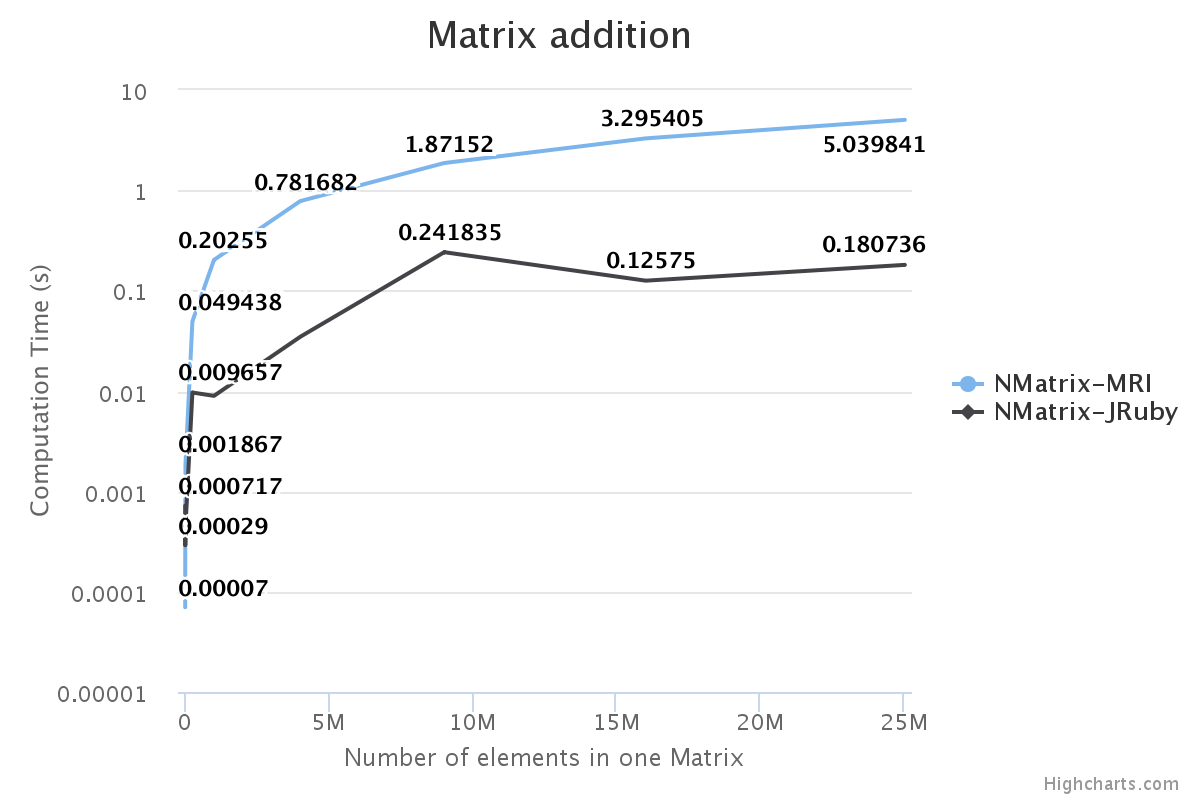
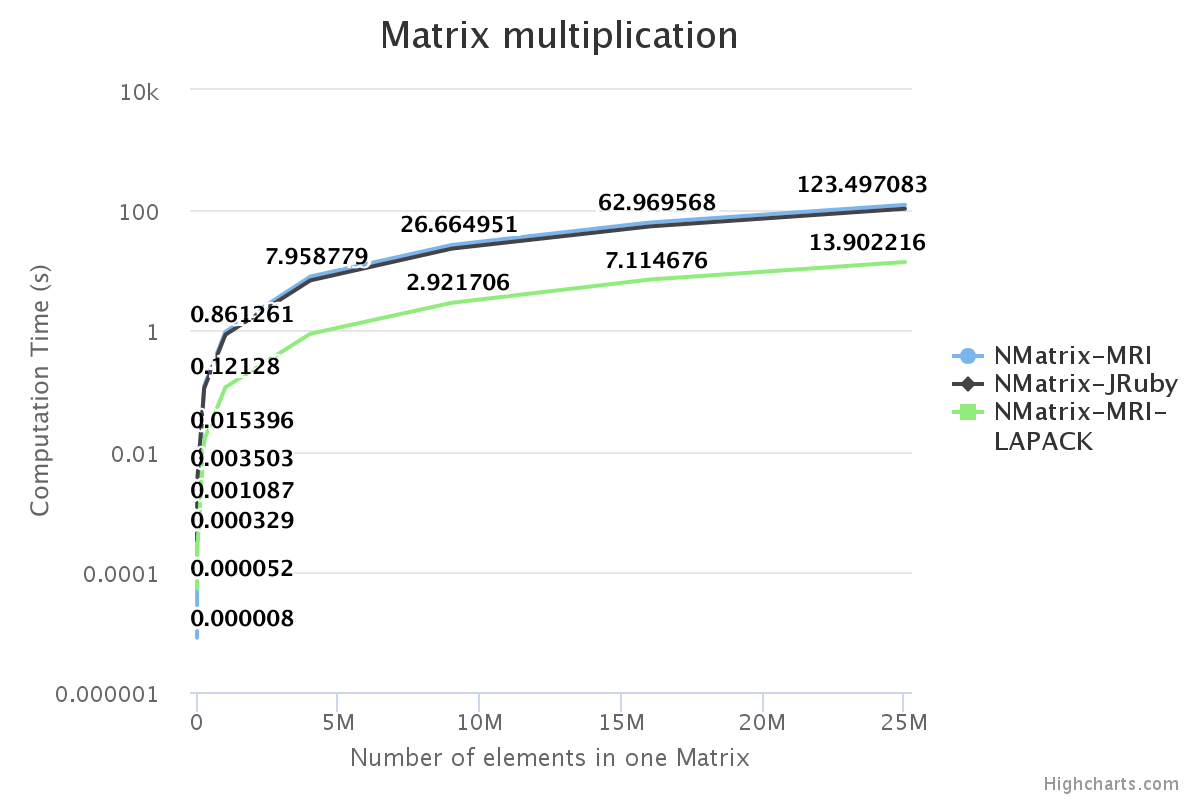
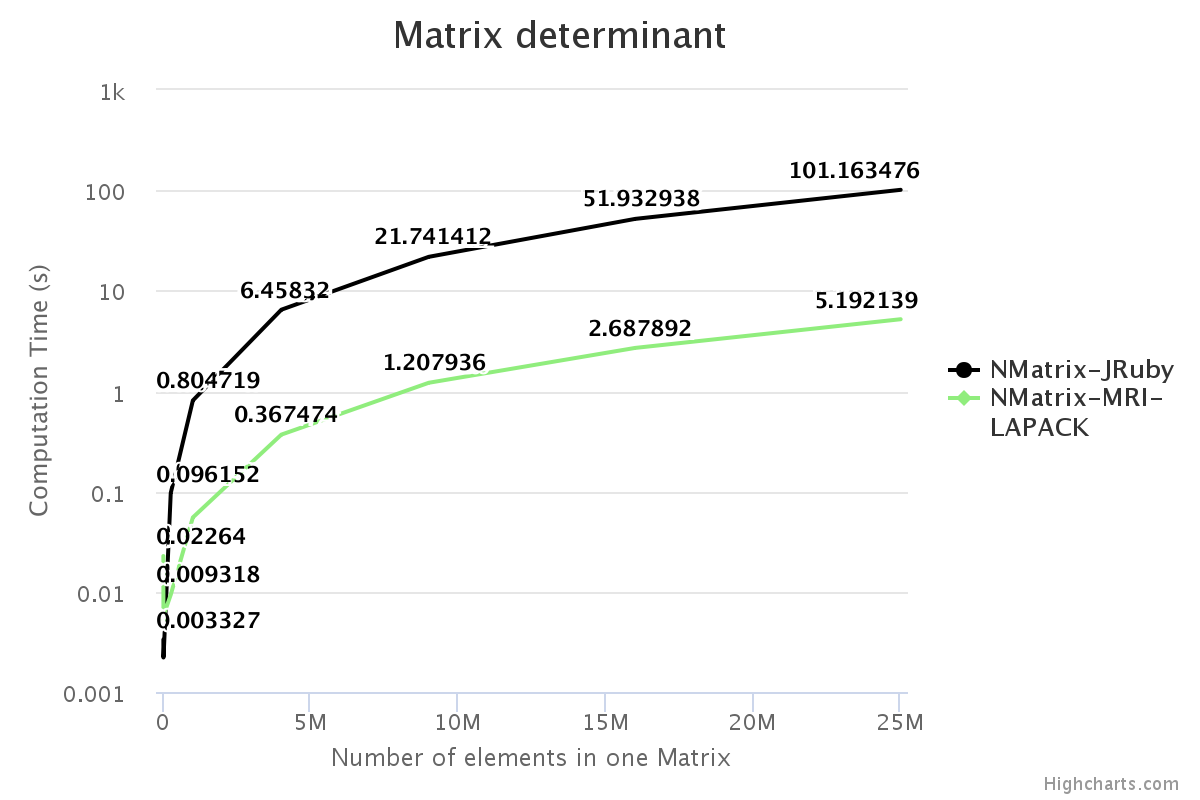
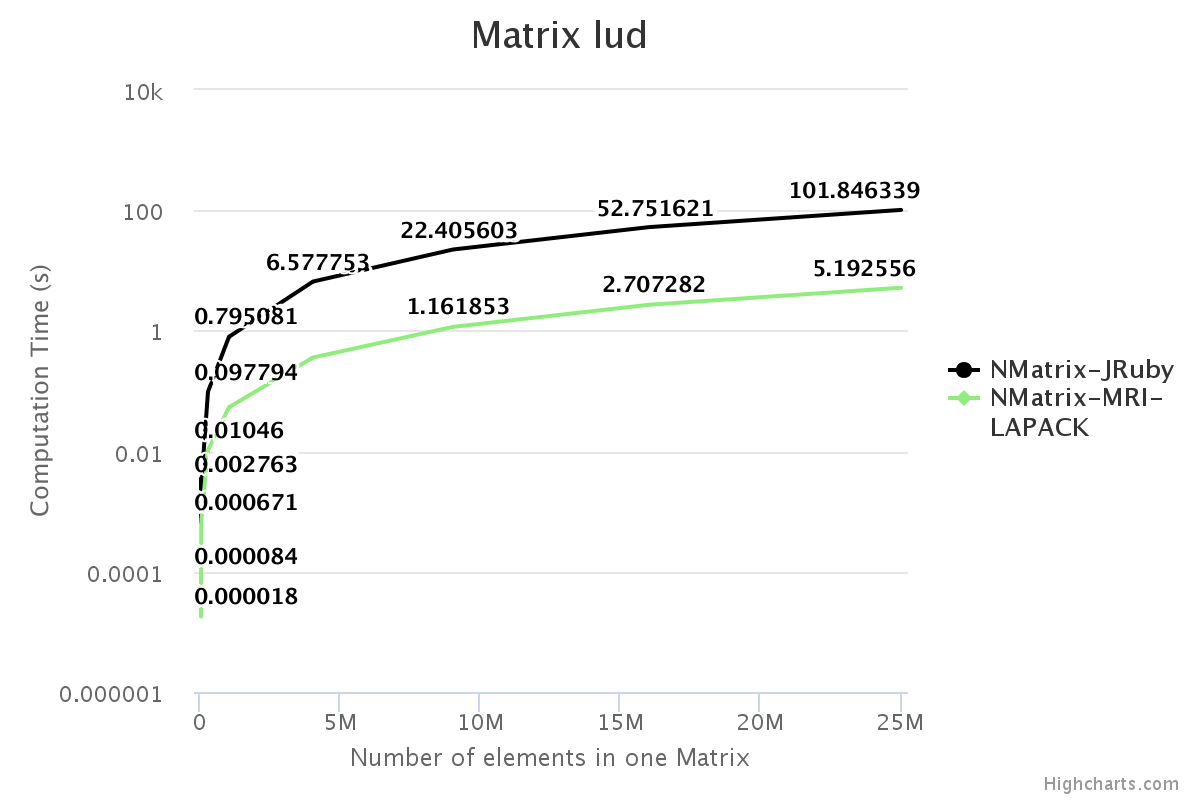
I have benchmarked some of the NMatrix functionalities. The following plots compare the performance between NMatrix-JRuby, NMatrix-MRI, and NMatrix-MRI using LAPACK/ATLAS libraries. (Note: MRI refers to the reference implementation of Ruby, for those who are new.)

Notes:

1. LAPACK and ATLAS aren’t involved in most element-wise operations, such as addition and subtraction.
2. NMatrix-MRI relies on LAPACK/ATLAS for calculating determinants and LU Decomposition (lud).

Result

1. For two-dimensional matrices, NMatrix-JRuby is currently slower than NMatrix-MRI for matrix multiplication and matrix decomposition functionalities (calculating determinant and factoring a matrix). NMatrix-JRuby is faster than NMatrix-MRI for other functionalities of a two-dimensional matrix — like addition, subtraction, trigonometric operations, etc.

2. NMatrix-JRuby is a clear winner when we are working with matrices of arbitrary dimensions.

Implementation

Storing n-dimensional matrices as one-dimensional arrays

The major components of an NMatrix are shape, elements, dtype and stype. When initialized, the dense type stores the elements as a one-dimensional array; in the JRuby port, the ArrayRealVector class is used to store the elements.

@s stores elements, @shape stores the shape of the matrix, while @dtype and @stype store the data type and storage type respectively. Currently, I have nmatrix-jruby implemented only for :float64 (double) and Ruby :object data types.

NMatrix-MRI uses struct as a type to store dim, shape, offset, count, src of an NMatrix. ALLOC and xfree are used to wrap the NMatrix attributes to C structs and release the unrequired memory.

Slicing and Rank

Implementing slicing was the toughest part of NMatrix-JRuby implementation. NMatrix@s stores the elements of a matrix as a one-dimensional array. The elements along any dimension are accessed with the help of the stride. NMatrix#get_stride calculates the stride with the help of the dimension and shape and returns an Array.

1
2
3
4
5
6
7
8
9
10

def get_stride(nmatrix)
  stride = Array.new()
  (0...nmatrix.dim).each do |i|
    stride[i] = 1;
    (i+1...dim).each do |j|
      stride[i] *= nmatrix.shape[j]
    end
  end
  stride
end

NMatrix#[] and NMatrix#[]= are thus able to read and write the elements of a matrix. NMatrix#MRI uses the @s object which stores the stride when the nmatrix is initialized.

NMatrix#[] calls the #xslice operator which calls #get_slice operator that use the stride to determine whether we are accessing a single element or multiple elements. If there are multiple elements, #dense_storage_get returns an NMatrix object with the elements along the dimension.

NMatrix-MRI differs from NMatrix-JRuby implementation as it makes sure that memory is properly utilized as the memory needs to be properly garbage collected.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def xslice(args)
  result = nil

  if self.dim < args.length
    raise(ArgumentError,"wrong number of arguments\
       (#{args} for #{effective_dim(self)})")
  else
    result = Array.new()
    slice = get_slice(@dim, args, @shape)
    stride = get_stride(self)
    if slice[:single]
      if (@dtype == :object)
        result = @s[dense_storage_get(slice,stride)]
      else
        s = @s.toArray().to_a
        result = @s.getEntry(dense_storage_get(slice,stride))
      end
    else
      result = dense_storage_get(slice,stride)
    end
  end
  return result
end

NMatrix#[]= calls the #dense_storage_set operator which calls #get_slice operator that use the stride to find out whether we are accessing a single element or multiple elements. If there are multiple elements #set_slice recursively sets the elements of the matrix then returns an NMatrix object with the elements along the dimension.

All the relevant code for slicing can be found here.

Enumerators

NMatrix-MRI uses the C code for enumerating the elements of a matrix. Just as with slicing, the NMatrix-JRuby uses pure Ruby code in place of the C code. Currently, all the enumerators for dense matrices with real data-type have been implemented and are properly functional. Enumerators for objects have not yet been implemented.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

def each_with_indices
  nmatrix = create_dummy_nmatrix
  stride = get_stride(self)
  offset = 0
  #Create indices and initialize them to zero
  coords = Array.new(dim){ 0 }

  shape_copy =  Array.new(dim)
  (0...size).each do |k|
    dense_storage_coords(nmatrix, k, coords, stride, offset)
    slice_index = dense_storage_pos(coords,stride)
    ary = Array.new
    if (@dtype == :object)
      ary << self.s[slice_index]
    else
      ary << self.s.toArray.to_a[slice_index]
    end
    (0...dim).each do |p|
      ary << coords[p]
    end

    # yield the array which now consists of the value and the indices
    yield(ary)
  end if block_given?
  nmatrix.s = @s

  return nmatrix
 end

Two-Dimensional Matrices

Linear algebra is mostly about two-dimensional matrices. In NMatrix, when performing calculations in a two-dimensional matrix, a one-dimensional array is converted to a two-dimensional matrix. A two-dimensional matrix is stored in the JRuby implementation as a BlockRealMatrix or Array2DRowRealMatrix. Each has its own advantages.

Getting a 2D Matrix

1
2
3
4
5
6
7
8
9
10
11
12
13
14

public class MatrixGenerator
{
  public static double[][] getMatrixDouble(double[] array, int row, int col)
  {
    double[][] matrix = new double[row][col];
    for (int index=0, i=0; i < row ; i++){
        for (int j=0; j < col; j++){
            matrix[i][j]= array[index];
            index++;
        }
    }
    return matrix;
  }
}

Convert a 2D-matrix to 1D-array

1
2
3
4
5
6
7
8
9
10
11
12
13
14

public class ArrayGenerator
{
  public static double[] getArrayDouble(double[][] matrix, int row, int col)
  {
    double[] array = new double[row * col];
    for (int index=0, i=0; i < row ; i++){
        for (int j=0; j < col; j++){
            array[index] = matrix[i][j];
            index++;
        }
    }
    return array;
  }
}

Why use a Java method instead of Ruby method?

1. Memory Usage and Garbage Collection: A scientific library is memory intensive and hence, every step counts. The JRuby interpreter doesn’t need to dynamically guess the data type and uses less memory, typically around one-tenth of it. If the memory is properly utilized, when the GC kicks in, the GC has to clear less used memory space.

2. Speed: Using java method greatly improves the speed — by around 1000 times, when compared to using the Ruby method.

Operators

All the operators from NMatrix-MRI have been implemented except modulus. The binary operators were easily implemented through Commons Math API and Java Math API.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def +(other)
  result = create_dummy_nmatrix
  if (other.is_a?(NMatrix))
    #check dimension
    raise(ShapeError, "Cannot add matrices with different dimension")\
    if (@dim != other.dim)
    #check shape
    (0...dim).each do |i|
      raise(ShapeError, "Cannot add matrices with different shapes") \
      if (@shape[i] != other.shape[i])
    end
    result.s = @s.copy.add(other.s)
  else
    result.s = @s.copy.mapAddToSelf(other)
  end
  result
end

Unary Operators (Trigonometric, Exponentiation and Log operators) have been implemented using #mapToSelf method that takes a Univariate function as an argument. #mapToSelf maps every element of ArrayRealVector object to the Univariate function, that is passed to it and returns self object.

1
2
3
4
5

def sin
  result = create_dummy_nmatrix
  result.s = @s.copy.mapToSelf(Sin.new())
  result
end

NMatrix#method(arg) has been implemented using bivariate functions provided by Commons Math API and Java Math API.

1
2
3
4
5

def gamma
  result = create_dummy_nmatrix
  result.s = ArrayRealVector.new MathHelper.gamma(@s.toArray)
  result
end

1
2
3
4
5
6
7
8
9
10
11
12
13

import org.apache.commons.math3.special.Gamma;

public class MathHelper{
  ...
  public static double[] gamma(double[] arr){
    double[] result = new double[arr.length];
    for(int i = 0; i< arr.length; i++){
      result[i] = Gamma.gamma(arr[i]);
    }
    return result;
  }
  ...
}

Decomposition

NMatrix-MRI relies on LAPACK and ATLAS for matrix decomposition and solving functionalities. Apache Commons Math provides a different set of API for decomposing a matrix and solving an equation. For example, #potrf and other LAPACK specific functions have not been implemented as they are not required at all.

Calculating determinant in NMatrix is tricky where a matrix is reduced either to a lower or upper matrix and the diagonal elements of the matrix are multiplied to get the result. Also, the correct sign of the result (whether positive or negative) is taken into account while calculating the determinant. However, NMatrix-JRuby uses Commons Math API to calculate the determinant.

1
2
3
4
5
6
7

def det_exact
  if (@dim != 2 || @shape[0] != @shape[1])
    raise(ShapeError, "matrices must be square to have a determinant defined")
    return nil
  end
  to_return = LUDecomposition.new(self.twoDMat).getDeterminant()
end

Given below is code that shows how Cholesky decomposition has been implemented by using Commons Math API.

Cholesky Decomposition

1
2
3
4
5
6
7
8
9
10
11
12
13

  def factorize_cholesky
    cholesky = CholeskyDecomposition.new(self.twoDMat)
    l = create_dummy_nmatrix
    twoDMat = cholesky.getL
    l.s = ArrayRealVector.new(ArrayGenerator.getArrayDouble\
        (twoDMat.getData, @shape[0], @shape[1]))

    u = create_dummy_nmatrix
    twoDMat = cholesky.getLT
    u.s = ArrayRealVector.new(ArrayGenerator.getArrayDouble\
      (twoDMat.getData, @shape[0], @shape[1]))
    return [u,l]
  end

Similarly, LU Decomposition and QR factorization have been implemented.

LU Decomposition

Code

QR Factorization

Code

NMatrix#solve

The solve method currently uses LU and Cholesky decomposition.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

  def solve(b, opts = {})
    raise(ShapeError, "Must be called on square matrix")\
       unless self.dim == 2 && self.shape[0] == self.shape[1]
    raise(ShapeError, "number of rows of b must equal number\
       of cols of self") if self.shape[1] != b.shape[0]
    raise(ArgumentError, "only works with dense matrices") if self.stype != :dense
    raise(ArgumentError, "only works for non-integer, non-object dtypes")\
       if integer_dtype? or object_dtype? or b.integer_dtype? or b.object_dtype?

    opts = { form: :general }.merge(opts)
    x    = b.clone
    n    = self.shape[0]
    nrhs = b.shape[1]

    nmatrix = create_dummy_nmatrix
    case opts[:form]
    when :general, :upper_tri, :upper_triangular, :lower_tri, :lower_triangular
      #LU solver
      solver = LUDecomposition.new(self.twoDMat).getSolver
      nmatrix.s = solver.solve(b.s)
      return nmatrix
    when :pos_def, :positive_definite
      solver = Choleskyecomposition.new(self.twoDMat).getSolver
      nmatrix.s = solver.solve(b.s)
      return nmatrix
    else
      raise(ArgumentError, "#{opts[:form]} is not a valid form option")
    end

  end

NMatrix#matrix_solve

Suppose we need to solve a system of linear equations:

                    AX = B

where A is an m×n matrix, B and X are n×p matrices, we need to solve this equation by iterating through B.

NMatrix-MRI implements this functionality using NMatrix::BLAS::cblas_trsm method. However, for NMatrix-JRuby, NMatrix#matrix_solve is the analogous method used.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

  def matrix_solve rhs
    if rhs.shape[1] > 1
      nmatrix = NMatrix.new :copy
      nmatrix.shape = rhs.shape
      res = []
      #Solve a matrix and store the vectors in a matrix
      (0...rhs.shape[1]).each do |i|
        res << self.solve(rhs.col(i)).s.toArray.to_a
      end
      #res is in col major format
      result = ArrayGenerator.getArrayColMajorDouble \
         res.to_java :double, rhs.shape[0], rhs.shape[1]
      nmatrix.s = ArrayRealVector.new result

      return nmatrix
    else
      return self.solve rhs
    end
  end

Currently, Hessenberg transformation for NMatrix-JRuby has not been implemented.

Other dtypes

I have tried implementing float dtypes using FloatMatrix class provide by jblas. jblas was used instead of Commons Math as the latter uses Field Elements for Floats and it had some issues with Reflection and Type Erasure. However, using jblas resulted in errors due to precision.

Code Organisation and Deployment

To minimise conflict with the MRI codebase all the JRuby front end code has been placed in the /lib/nmatrix/jruby directory. lib/nmatrix/nmatrix.rb decides whether to load nmatrix.so or nmatrix_jruby.rb after detecting the Ruby platform.

The added advantage is that the Ruby interpreter must not decide which function to call at run-time. The impact on performance can be seen when programs which intensively use NMatrix for linear algebraic computations (e.g., mixed_models) are run.

Spec Report

After the port; this is the final report that summarizes the number of tests that successfully pass:

NMatrix

Why do some tests fail?

1. Complex dtype has not been implemented.
2. Sparse matrices (list and yale) have not been implemented.
3. Decomposition methods that are specific to LAPACK and ATLAS have not been implemented.
4. Integer dtype is not properly assigned to floor, ceil, and round methods.

Mixed_Models

Future Work

NMatrix on JRuby offers comparable speeds to MRI. For specific computations it will be possible to leverage the threading support of JRuby and speed up things using multiple cores.

Adding new functionality to NMatrix-JRuby will be easy from here. Personally, I am interested to add OpenCL support to leverage the GPU computational capacity available on most machines today.

Conclusion

The main goal of this project was to to gain from the performance JRuby offers, and bring a unified interface for linear algebra between MRI and JRuby.

By the end of GSoC, I have been able to successfully create a linear algebra library, NMatrix for JRuby users, which they can easily run on their machines — unless they want to use complex numbers, at least for now.

I have mixed_models gem simultaneously ported to JRuby. Even here, NMatrix-JRuby is very close to NMatrix-MRI, considering the performance .

Acknowledgements

I would like to express my sincere gratitude to my mentor Pjotr Prins for the continuous support through the summers, and for his patience, motivation, enthusiasm, and immense knowledge. I could not have imagined having a better advisor and mentor, for this project.

I am very grateful to Google and the Ruby Science Foundation for this golden opportunity.

I am very thankful to Charles Nutter, John Woods, Sameer Deshmukh, Kenta Murata and Alexej Gossmann, who mentored me through the project. It has been a great learning experience.

I thank my fellow GSoC participants Rajith, Lokesh and Gaurav who helped me with certain aspects of my project.